[알고리즘] 동적계획법(DP)

개념

큰 문제를 여러개의 작은 문제로 나눠서 푸는 알고리즘

• 메모이제이션을 이용하면 큰 문제로부터 빠른 속도로 최적의 해를 찾아낼 수 있다.

• DP의 대표 예시인 피보나치 수열에서 7번째 값을 구하고 싶다고 가정하면,

  

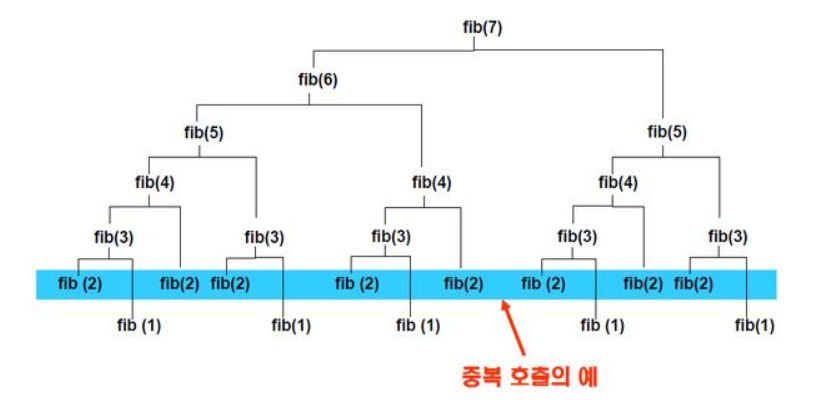
  위 그림과 같이 중간에 중복 호출이 발생하기 때문에 메모이제이션(Memoization) 기법을 사용해줘야 한다.

메모이제이션

반복되는 결과를 메모리에 저장해서 중복호출 되었을 때, 한번 더 계산하지 않고 메모리에 저장한걸 가져와 재활용하는 기법

• 장점: 큰 문제로부터 빠른 속도로 최적의 해를 찾아낼 수 있다.

구현

Top-Down, Bottom-Up의 두가지 방법이 있다.

1. Top-Down

큰 문제에서 작은 문제를 재귀적으로 호출하여 리턴된 값으로 문제를 해결하는 방식

func(n) = func(n-1) + func(n-2);

• (장점)메모이제이션을 잘 활용하면 Bottom-Up방식 보다 훨씬 빠르다.
• (단점)재귀 함수를 구현하므로 함수 호출에 대한 오버헤드가 발생한다.

2. Bottom-Up

작은 부분 문제를 미리 계산해두고, 이 문제들을 모아 큰 문제를 해결하는 방식

DP[1] = 1;
DP[2] = 1;

for(int i=3; i<N; i++) DP[i] = DP[i-2] + DP[i-1];

• (장점) for문으로 구현되므로 자원에 비교적 자유로워서 시간 및 메모리 최적하가 쉽다.
• (단점) 모든 부분 문제를 해결해야 한다.

응용

1. 피보나치수
2. KnapSack
3. LCS
4. LIS
5. Edit Distance
6. Matrix Chain Multiplication

1. 피보나치수

1 1 2 3 5 8… 이런 식으로 N번째의 값 = N-1번째 값 + N-2번째 값을 계산하는 수열

… 추가예정