[자료구조] 분할정복(Division and conquest)

개념

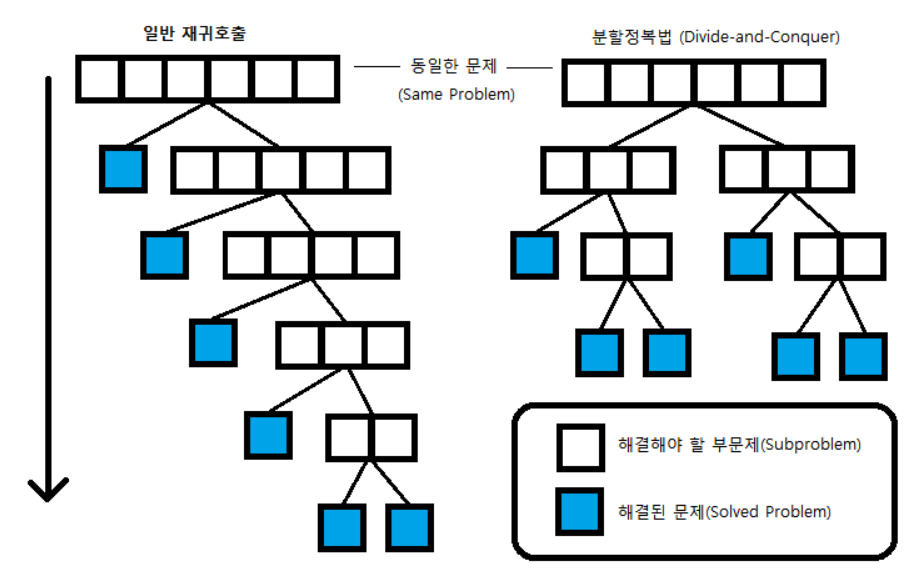
주어진 문제를 작은 사례로 나누고(Divide) 각각의 작은 문제들을 해결하여 정복(Conquer)하는 방법

• 하향식(Top-down) 접근방법

👍장점

• 문제를 나눔으로써 어려운 문제 해결 가능
• 병렬적으로 문제를 해결하는데 큰 강점

👎단점

• 함수 재귀 호출로 인한 오버헤드가 발생
• 스택 오버플로우가 발생으로 과도한 메모리 사용

순서

1. 분할(Divide): 해결할 문제를 여러 개의 작은 부분으로 나눈다.
2. 정복(Conquer): 나눈 작은 문제를 각각 해결한다.
3. 통합(Combine): (필요하다면) 해결된 해답을 모은다.

응용

거듭제곱, 이분탐색, 합병정렬, 퀵정렬, 최대값 찾기 등

거듭제곱

x의 n승을 구해보자
⇒ 반복문으로 해결할 수 있지만, n이 커지게 되면 반복의 수행횟수가 늘어난다.
⇒ 분할 정복 알고리즘을 적용해보자

n이 짝수일때와 홀수일때로 나누어서 생각한다.

• 짝수: x^n/2 * x^n/2 * x
• 홀수: x^n/2 * x^n/2 * x
• 기저조건: 지수가 1이 되면 더 이상 나눌 수 없다.
• 시간복잡도: logN
  ⇒ 반의 반의 반..으로 계속 줄면서 문제가 해결되므로 밑수를 2로 하는 logN이다.

import java.util.Scanner;

public class Main {
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int x = sc.nextInt();
		int y = sc.nextInt(); //지수
		System.out.println(exp(x, y));
	}

	private static int exp(int x, int y) {
		
		if(y == 1) return x;
		int result = exp(x, y/2); //절반에 해당하는 제곱승을 가져와서
		result *= result;//자기자신에게 곱합 => y
		
		if(y % 2 != 0) { //이 때, y가 홀수인 경우
			result *= x;
		}
		
		return result;
	}
}